前言:2025年台灣與香港債券市場,為何 Duration 與 Convexity 如此重要?
全球經濟形勢不斷變化,預計2025年的利率環境將充滿不確定性,這對債券投資者來說帶來了挑戰,同時也蘊藏機會。不論是台灣的散戶投資人、香港的財富管理專家,還是金融業從業者,都需要清楚掌握債券價格如何回應利率波動,這是有效應對債券市場的核心。在這樣的背景下,債券存續期間與債券凸性這兩個指標,成為評量利率風險和預期報酬的關鍵武器。
存續期間給出利率敏感度的初步評估,例如利率每變動1%,債券價格可能出現的變化幅度。但這種線性估計在利率劇烈波動時會失準,這時凸性就能補足缺口,更準確捕捉債券價格的彎曲反應。本文將詳細探討這兩個概念的定義、計算方法、差異、意義,以及在2025年台灣和香港投資實務中的應用,幫助您制定更智慧的策略。
透過這些工具,您不僅能更好地理解市場動態,還能在不穩定的利率環境中保護資產並抓住獲利時機。接下來,我們一步步拆解這些概念,讓投資變得更具洞察力。
債券存續期間 是什麼?衡量利率風險的第一把尺
在債券投資的世界裡,存續期間是最基礎卻也至關重要的概念,它幫助我們量化債券價格對利率變化的反應程度。
存續期間的定義與基本概念
存續期間簡單講,就是投資本金加權平均回收時間,它直觀地反映了利率風險的程度。當市場利率上漲時,存續期間較長的債券價格通常會大幅下滑;反之亦然。以存續期間為5年的債券為例,利率上升1%可能導致價格下跌約5%,而利率下降1%則可能帶來相應的5%漲幅。這種衡量讓投資者能快速評估潛在波動。
三種常見的存續期間:修正、麥考利與有效存續期間
實務上,存續期間有不同類型,最常見包括麥考利存續期間、修正存續期間以及有效存續期間:
- 麥考利存續期間: 這是存續期間的原創理論,由加拿大經濟學家弗雷德里克·麥考利發明。它透過計算債券未來現金流(票息加本金)的現值加權平均,得出回收投資的平均年數。單位為年,假設殖利率不變,且現金流以該率再投資。
- 修正存續期間: 這是最實用的一種,從麥考利存續期間衍生,直接估計到期殖利率每變1%時,債券價格的百分比變化。公式為:
修正存續期間 = 麥考利存續期間 / (1 + 到期殖利率 / 每年付息次數)
它適用於固定利率債券,假設利率變化不影響現金流。 - 有效存續期間: 對於內含選擇權的債券,如可贖回或可賣回債券,利率變化可能觸發行使權利,改變現金流。此時修正存續期間失效,有效存續期間則透過模擬不同利率下的價格變化來計算,提供更可靠的敏感度評估。
存續期間的影響因素與限制
存續期間受幾個主要因素左右:
- 到期年限: 年限越長,存續期間通常越長,利率風險隨之放大。
- 票面利率: 票面利率低,回收本金時間拉長,存續期間也較長。零息債券的存續期間正好等於到期年限,是風險最高的類型。
- 到期殖利率: 殖利率越高,現金流現值權重越小,存續期間傾向縮短。
儘管如此,存續期間的線性假設有其侷限,在利率小變動時有效,但大幅波動時預測會偏差。這就需要凸性來調整。
債券凸性 是什麼?修補存續期間誤差的第二把尺
當利率大幅震盪,單用存續期間預測價格變化往往不準,這時凸性成為不可或缺的補充工具。
凸性的定義與重要性
凸性捕捉債券價格對利率變化的彎曲反應,相當於存續期間變化的速率。如果存續期間是速度,凸性就是加速度。它讓我們在利率劇變時,更好地預測價格走勢。高正凸性對投資者有利,因為利率跌時價格漲得更多,漲時跌得更少,提供天然保護。
正凸性與負凸性:了解你的債券特性
債券凸性分正負,影響風險報酬格局:
- 正凸性: 傳統固定利率債券多具此特性。利率下降時,價格漲幅超存續期間預期;上升時,跌幅小於預期。這給投資者額外緩衝和上漲空間。
- 負凸性: 常見於可贖回債券,發行人有權在利率低時提前贖回。利率跌時,投資者無法全享漲幅;漲時則承擔全額損失。這不利投資,放大下行風險。
凸性計算公式與意義
凸性計算基於價格對殖利率的二階導數,公式為:
凸性 = [1 / 價格 * (d²價格 / dYTM²)]
實務中多用軟體計算。意義在於量化價格曲線的彎度,高凸性意味更大修正效果。結合存續期間的預測公式為:
%ΔP ≈ (-修正存續期間 %ΔYTM) + (0.5 凸性 * (%ΔYTM)²)
這二次項在利率大變時特別有用。
影響凸性的因素
凸性因素與存續期間類似,但強調不同:
- 到期年限: 長年限帶來更高凸性,曲線彎度更大。
- 票面利率: 低票面或零息債券凸性最高。
- 到期殖利率: 低殖利率提升凸性。
- 選擇權條款: 可贖回引入負凸性,可賣回則強化正凸性。
債券 Duration vs Convexity:兩大指標的關鍵差異與互補關係
要精通債券投資,必須比較存續期間與凸性的異同,以及它們如何互補。
核心功能與衡量重點比較
| 特性 | 債券存續期間 (Duration) | 債券凸性 (Convexity) |
| :————- | :—————————————— | :———————————————- |
| 核心功能 | 衡量利率變動1%時債券價格的預期百分比變動。 | 衡量利率大幅變動時債券價格變動的「加速」或「減速」效應。 |
| 衡量重點 | 利率敏感度的「線性」近似。 | 利率敏感度的「非線性」反應,修補 Duration 的誤差。 |
| 預測準確性 | 利率小幅變動時較準確。 | 利率大幅變動時提供更精確的預測。 |
| 投資者偏好 | 較短 Duration 通常風險較低。 | 高正 Convexity 通常受投資者青睞。 |
| 單位 | 年或百分比 (修正存續期間) | 無單位 (或可視為百分比的平方) |
圖解說明:存續期間的直線與凸性的曲線
試想債券價格與利率的圖表:存續期間畫出直線,代表線性關係。但實際曲線是彎的。
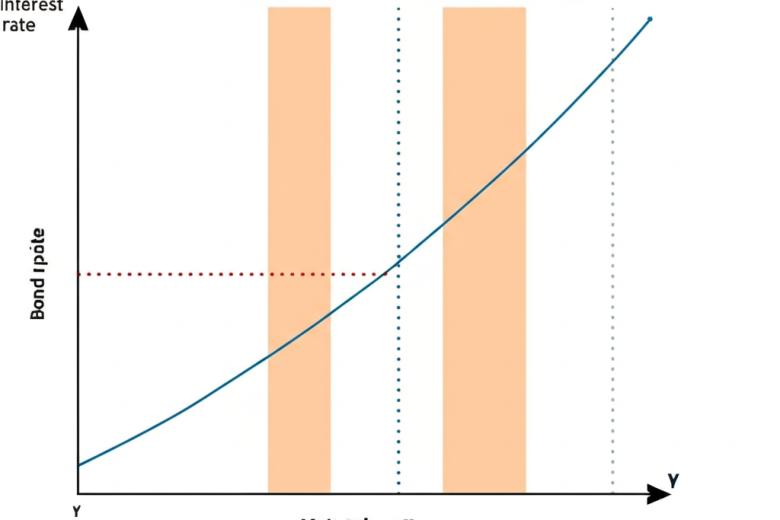
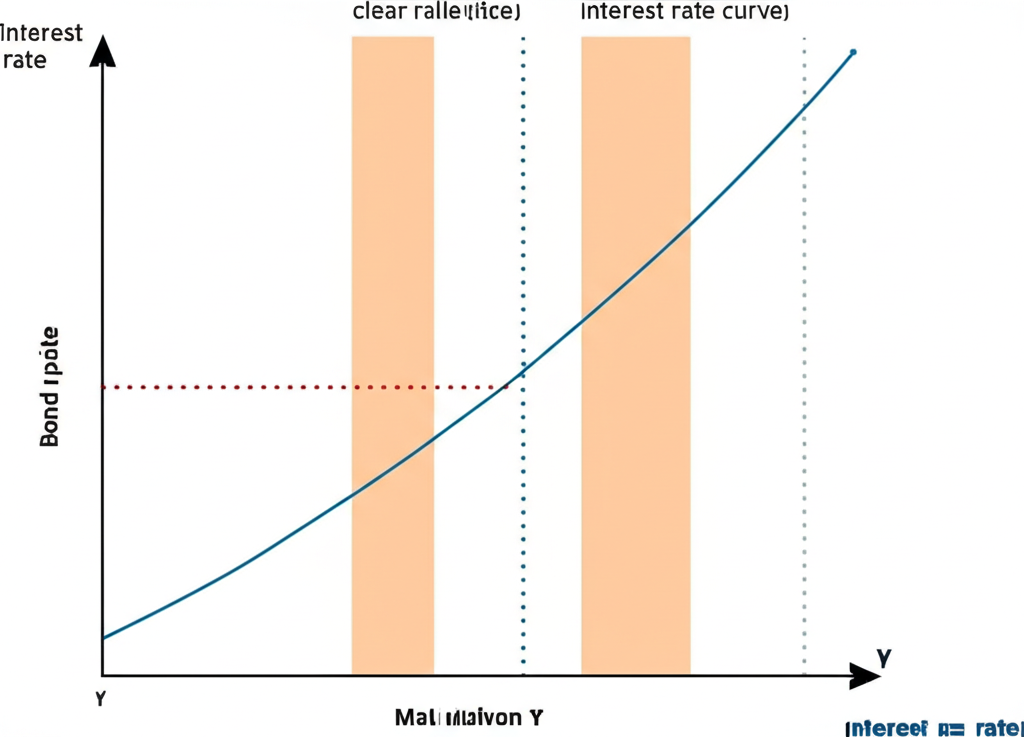
圖1: 利率與債券價格關係示意圖
(此處應插入一張圖表,X軸為市場利率,Y軸為債券價格。圖中應包含一條代表存續期間預測的直線,以及一條代表實際債券價格變動的彎曲曲線。在利率下降時,實際曲線位於直線之上;在利率上升時,實際曲線也位於直線之上,展示正凸性效應。曲線與直線之間的垂直距離即為凸性對預測的修正。)
如圖所示,小變動時直線準確,但大變動時偏差明顯。凸性捕捉這彎曲,讓預測更貼近現實。正凸性曲線向上彎,帶來優勢。
為何兩者缺一不可?更精準的風險評估
只用存續期間在波動市場易誤判,例如高估跌幅或低估漲幅。凸性修正這些,讓評估全面。結合使用,能全面理解風險,避免失誤。
2025年台灣與香港投資者:如何應用 Duration 與 Convexity 於債券策略?
2025年,全球經濟與利率變化將持續影響台灣和香港債券市場。投資者需善用存續期間與凸性,打造穩健組合。
市場展望與利率情境:台灣/香港的視角
到2024年底,市場預期美國聯準會升息接近尾聲,2025年或轉降息。這波及台灣央行與香港金管局。台灣央行2024年3月意外加息半碼,防範通膨;香港則跟隨美國匯率制度。
在利率趨穩或微降情境下,投資者應注意:
- 降息預期: 長存續期間債券漲幅潛力大。
- 利率波動: 不確定性高時,高正凸性債券更優。
根據 金融時報 報導,央行政策將深刻影響債券市場,平衡通膨與增長。
風險管理實戰:降低利率風險的策略
台灣與香港投資者可透過以下方式應用這些指標:
- 長短期債券配置:
- 預期降息或利率持穩: 提高長存續期間債券比重,如台灣長期公債或優質公司債,捕捉價格上漲。
- 預期升息或利率波動大: 轉向短存續期間債券,減輕上漲衝擊。
- 高凸性債券的優勢: 波動環境下,高正凸性提供保護與潛力。雖零息債最高,但在本地市場,可分散中長期固定收益產品。
- 避開負凸性陷阱: 警惕可贖回債券,利率降時易遭贖回,面臨再投資風險。評估時讀條款,用有效存續期間檢查。
案例分析:台灣投資者如何運用兩者評估投資組合
假設台灣投資者小陳持有兩檔債券:
債券 A: 台灣5年期公債,修正存續期間 = 4.5年,凸性 = 25。
債券 B: 某台灣上市電子公司發行的10年期公司債(含發行者可贖回條款),修正存續期間 = 7年,凸性 = -10。
情境分析:
- 若預期利率小幅下降0.5%:
- 債券 A:價格預計上漲約 4.5% * 0.5% = 2.25%。
- 債券 B:價格預計上漲約 7% * 0.5% = 3.5%。
小變動時,凸性影響小,B債券因長期間表現佳。
- 若預期利率大幅下降2%:
- 債券 A(高正凸性):價格變動 ≈ (-4.5 -2%) + (0.5 25 (-2%)²) = 9% + (0.5 25 * 0.0004) = 9% + 0.5% = 9.5%。漲幅超線性預測。
- 債券 B(負凸性):價格變動 ≈ (-7 -2%) + (0.5 -10 (-2%)²) = 14% – (0.5 10 * 0.0004) = 14% – 0.2% = 13.8%。負凸性限制漲幅,贖回風險更甚。
大變動時,A債券憑正凸性勝出。
此例顯示,單看存續期間不足,凸性在波動中至關重要。
常見誤區與專業建議:提升你的債券投資洞察力
即使資深投資者,也常對存續期間與凸性有誤解。釐清這些,能精進決策。
誤區一:只看存續期間,忽略凸性
許多人以為存續期間足夠掌握風險,但它僅線性近似,大變動時易錯。
專業建議: 總是合用兩者。同期間下,選高正凸性債券,在波動中獲更好收益或減損。
誤區二:將存續期間等同於到期年限
兩者單位皆年,但不同。到期年限固定,存續期間動態考量票息。只有零息債等同。
專業建議: 視存續期間為風險指標,到期年限為時間框架。決策時優先存續期間。
專業建議:動態調整與持續學習
債券市場動盪,投資者需:
- 動態調整投資組合: 定期檢視整體存續期間與凸性。預期降息增長期間;波動大選高正凸性。
- 關注市場指標: 追蹤美聯儲、歐央行政策,以及台灣香港數據。香港金管局的 月度回顧與報告 提供寶貴洞見。
- 持續學習: 市場產品複雜,熟練基礎並探複雜工具,提升能力。
結論:2025年掌握 Duration 與 Convexity,穩健前行台灣債券市場
2025年債券市場機會與風險並存,存續期間與凸性是台灣香港投資者的利器。前者奠基敏感度評估,後者修正線性誤差,尤其大波動時精準預測,助避險獲利。
善用它們,您能:
- 精準評估組合利率風險。
- 依利率展望調整配置。
- 避開負凸性債券。
- 選高正凸性優化收益。
在變幻市場,融入這些概念是穩健投資、最大化報酬的關鍵。祝您運用所長,智慧決策,穩步成長財富。
1. 債券存續期間 (Duration) 和債券凸性 (Convexity) 最主要的差異是什麼?
債券存續期間衡量的是債券價格對利率變動的「線性」敏感度,即利率變動1%時,債券價格預期的百分比變動。而債券凸性則衡量的是這種敏感度的「非線性」部分,或者說是存續期間本身的變化率。它修補了存續期間在利率大幅變動時的預測誤差,提供了更精確的價格變動預期。
2. 為什麼在評估債券投資時,不能只看存續期間而忽略凸性?
單獨使用存續期間進行評估,其假設利率與債券價格呈線性關係,這在利率小幅變動時相對準確。然而,當利率大幅變動時,實際的債券價格變動會偏離這種線性預測。忽略凸性可能導致您低估利率風險或高估潛在收益,尤其是在市場波動劇烈時。
3. 什麼是修正存續期間?它和麥考利存續期間有何不同?
麥考利存續期間 (Macaulay Duration) 是債券所有未來現金流按現值加權後,收回投資本金的平均時間,其單位是「年」。它是存續期間的理論基礎。修正存續期間 (Modified Duration) 則由麥考利存續期間推導而來,是實務上最常用的指標,直接衡量當到期殖利率變動1%時,債券價格預期的百分比變動。
4. 債券凸性公式是如何計算的?它代表什麼意義?
債券凸性的計算涉及債券價格對到期殖利率的二階導數,數學上較為複雜,通常由專業軟體計算。其意義在於衡量債券價格曲線的彎曲程度。高正凸性意味著在利率下降時,債券價格上漲幅度會比線性預測更多;在利率上升時,價格下跌幅度會比線性預測更少,為投資者帶來額外優勢。
5. 在2025年台灣市場,高存續期間的債券是否一定風險較高?
高存續期間的債券確實意味著對利率變動的敏感度較高,因此在利率上升時,其價格下跌的幅度會較大,風險相對較高。然而,若您預期2025年利率將下降或維持低位,高存續期間的債券則可能帶來較高的價格上漲潛力。風險與收益總是並存,關鍵在於您的利率展望和風險承受能力。
6. 負凸性債券有哪些?投資這類債券需要注意什麼風險?
具有負凸性的債券主要是那些含有嵌入式選擇權的債券,最常見的是「可贖回債券 (Callable Bonds)」。這類債券賦予發行者在利率下降時提前贖回債券的權利。投資負凸性債券的主要風險是「再投資風險」:當利率下降時,發行者可能贖回債券,迫使投資者在更低的利率環境下重新投資,限制了您的潛在收益。
7. 如何利用存續期間和凸性來構建一個更穩健的債券投資組合?
構建穩健組合的關鍵在於平衡。您可以:
- 根據對利率走勢的預期,調整投資組合的整體存續期間。例如,預期降息則增加長存續期間債券。
- 在同等存續期間下,偏好具有較高正凸性的債券,以在利率波動時獲得更好的風險調整收益。
- 分散投資不同到期年限和票面利率的債券,以控制整體組合的存續期間和凸性。
- 避免過度集中於負凸性債券,或在投資前充分理解其風險。
8. 利率大幅變動時,存續期間的預測誤差為何需要凸性來修正?
存續期間假設利率與債券價格呈直線關係,但實際的價格曲線是彎曲的。當利率大幅變動時,這條直線預測會與實際曲線產生較大偏差。凸性作為價格曲線的彎曲度量,能捕捉這種非線性關係,從而在存續期間的基礎上,提供一個更接近實際價格變動的二次項修正,使預測更為精準。
9. 浮動利率債券的存續期間和凸性與固定利率債券有何不同?
浮動利率債券的票面利率會根據市場利率(如LIBOR或TAIBOR)定期調整,因此其價格對利率變動的敏感度遠低於固定利率債券。通常,浮動利率債券的修正存續期間會非常短(接近於下一個付息日),其凸性也相對較低。這使得它們在升息環境下更具吸引力,因為能減少利率上升帶來的價格損失。
10. 投資新手應該如何理解和應用債券存續期間與凸性?
投資新手可以將存續期間理解為「債券對利率變化的敏感度計」,數值越大越敏感。凸性則可視為「敏感度計的校準器」,它讓您在利率變化大時,能更準確地預估實際情況。應用上,新手可以從以下幾點開始:
- 從理解基本定義和影響因素入手。
- 在選擇債券產品時,除了到期年限和票面利率,也查詢其存續期間和凸性數據。
- 在利率前景不明朗或預期波動較大時,可優先考慮短存續期間和高正凸性的債券,以降低風險。
- 持續關注金融市場新聞和專業分析,逐步將這些概念應用到您的投資決策中。